Разделы сайта
Выбор редакции:
- Крейсер "красный крым" черноморского флота
- «31 спорный вопрос» русской истории: житие императора Николая II
- Лечебные свойства корня лопуха и его широкое применение в домашних условиях
- Природные ресурсы западной сибири
- Совместимость петуха и змеи в любовных отношениях и браке Он петух она змея совместимость
- Чемерица черная: прекрасная и опасная Противопоказания и побочные действия
- Чем интересна Свято-Михайло-Афонская Закубанская пустынь?
- Порционная сельдь под шубой на праздничный стол
- К чему снится шить во сне
- Примета — разбить зеркало случайно: что делать, если оно треснуло
Реклама
| Свойства собственных чисел и векторов матрицы. Собственные значения (числа) и собственные векторы.Примеры решений |
|
Как вставить математические формулы на сайт? Если нужно когда-никогда добавлять одну-две математические формулы на веб-страницу, то проще всего сделать это, как описано в статье : математические формулы легко вставляются на сайт в виде картинок, которые автоматически генерирует Вольфрам Альфа. Кроме простоты, этот универсальный способ поможет улучшить видимость сайта в поисковых системах. Он работает давно (и, думаю, будет работать вечно), но морально уже устарел. Если же вы постоянно используете математические формулы на своем сайте, то я рекомендую вам использовать MathJax - специальную библиотеку JavaScript, которая отображает математические обозначения в веб-браузерах с использованием разметки MathML, LaTeX или ASCIIMathML. Есть два способа, как начать использовать MathJax: (1) при помощи простого кода можно быстро подключить к вашему сайту скрипт MathJax, который будет в нужный момент автоматически подгружаться с удаленного сервера (список серверов ); (2) закачать скрипт MathJax с удаленного сервера на свой сервер и подключить ко всем страницам своего сайта. Второй способ - более более сложный и долгий - позволит ускорить загрузку страниц вашего сайта, и если родительский сервер MathJax по каким-то причинам станет временно недоступен, это никак не повлияет на ваш собственный сайт. Несмотря на эти преимущества, я выбрал первый способ, как более простой, быстрый и не требующий технических навыков. Следуйте моему примеру, и уже через 5 минут вы сможете использовать все возможности MathJax на своем сайте. Подключить скрипт библиотеки MathJax с удаленного сервера можно при помощи двух вариантов кода, взятого на главном сайте MathJax или же на странице документации :
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax. Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта. Любой фрактал строится по определенному правилу, которое последовательно применяется неограниченное количество раз. Каждый такой раз называется итерацией. Итеративный алгоритм построения губки Менгера достаточно простой: исходный куб со стороной 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из него удаляются один центральный куб и 6 прилежащих к нему по граням кубов. Получается множество, состоящее из 20 оставшихся меньших кубов. Поступая так же с каждым из этих кубов, получим множество, состоящее уже из 400 меньших кубов. Продолжая этот процесс бесконечно, получим губку Менгера. СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ Системой однородных линейных уравнений называется система вида Ясно, что в этой случае Так как неизвестные находятся по формулам Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0. Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений. Примеры. 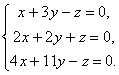 СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ Пусть задана квадратная матрица Во многих задачах приходится рассматривать уравнение относительно X где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение . Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A , а X при таком λ называется собственным вектором матрицы A . Найдём собственный вектор матрицы A
. Поскольку E
∙X = X
, то
матричное уравнение можно переписать в виде И, следовательно, Итак, получили систему однородных линейных уравнений для определения координат x 1 , x 2 , x 3 вектора X . Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.
Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ. Каждому собственному значению λ соответствует собственный вектор X , координаты которого определяются из системы при соответствующем значении λ. Примеры. ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА При изучении различных разделов физики встречаются величины, которые полностью определяются заданием их численных значений, например, длина, площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых, кроме численного значения, необходимо знать также их направление в пространстве, например, сила, действующая на тело, скорость и ускорение тела при его движении в пространстве, напряжённость магнитного поля в данной точке пространства и т.д. Такие величины называются векторными. Введём строгое определение. Направленным отрезком назовём отрезок, относительно концов которого известно, какой из них первый, а какой второй.
Вектором называется направленный отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если A – начало вектора, B – его конец, то вектор обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его направление стрелкой. Модулем или длиной вектора называют длину определяющего его направленного отрезка. Обозначается || или ||. К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и модуль его равен нулю ||=0. Векторы и называются коллинеарными , если они расположены на одной прямой или на параллельных прямых. При этом если векторы и одинаково направлены, будем писать , противоположно . Векторы, расположенные на прямых, параллельных одной и той же плоскости, называются компланарными . Два вектора и называются равными , если они коллинеарны, одинаково направлены и равны по длине. В этом случае пишут . Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства. Например . ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ Произведением вектора на число λ называется новый вектор такой, что: Произведение вектора на число λ обозначается .
Например, есть вектор, направленный в ту же сторону, что и вектор , и имеющий длину, вдвое меньшую, чем вектор . Введённая операция обладает следующими свойствами : Пусть и – два
произвольных вектора. Возьмём произвольную точку O
и
построим вектор . После этого из точки A
отложим вектор . Вектор , соединяющий начало первого вектора c концом
второго , называется суммой
этих векторов и обозначается
Сформулированное определение сложения векторов называют правилом параллелограмма , так как ту же самую сумму векторов можно получить следующим образом. Отложим от точки O векторы и . Построим на этих векторах параллелограмм ОАВС . Так как векторы , то вектор , являющийся диагональю параллелограмма, проведённой из вершины O , будет очевидно суммой векторов .
Легко проверить следующие свойства сложения векторов . Вектор, коллинеарный данному вектору , равный ему по длине и противоположно направленный, называется противоположным вектором для вектора и обозначается . Противоположный вектор можно рассматривать как результат умножения вектора на число λ = –1: . С матрицей А, если найдется такое число l, что АХ = lХ. При этом число l называют собственным значением оператора (матрицы А), соответствующим вектору Х. Иными словами, собственный вектор - это такой вектор, который под действием линейного оператора переходит в коллинеарный вектор, т.е. просто умножается на некоторое число. В отличие от него, несобственные векторы преобразуются более сложно. Запишем определение собственного вектора в виде системы уравнений: Перенесем все слагаемые в левую часть:
Последнюю систему можно записать в матричной форме следующим образом: (А - lЕ)Х = О Полученная система всегда имеет нулевое решение Х = О. Такие системы, в которых все свободные члены равны нулю, называют однородными . Если матрица такой системы - квадратная, и ее определитель не равен нулю, то по формулам Крамера мы всегда получим единственное решение - нулевое. Можно доказать, что система имеет ненулевые решения тогда и только тогда, когда определитель этой матрицы равен нулю, т.е. |А - lЕ| = Это уравнение с неизвестным l называют характеристическим уравнением (характеристическим многочленом ) матрицы А (линейного оператора). Можно доказать, что характеристический многочлен линейного оператора не зависит от выбора базиса. Например, найдем собственные значения и собственные векторы линейного оператора, заданного матрицей А = . Для этого составим характеристическое уравнение |А - lЕ| = Чтобы найти собственные векторы, решаем две системы уравнений (А + 5Е)Х = О (А - 7Е)Х = О Для первой из них расширенная матрица примет вид
откуда х 2 = с, х 1 + (2/3)с = 0; х 1 = -(2/3)с, т.е. Х (1) = (-(2/3)с; с). Для второй из них расширенная матрица примет вид
откуда х 2 = с 1 , х 1 - (2/3)с 1 = 0; х 1 = (2/3)с 1 , т.е. Х (2) = ((2/3)с 1 ; с 1). Таким образом, собственными векторами этого линейного оператора являются все вектора вида (-(2/3)с; с) с собственным значением (-5) и все вектора вида ((2/3)с 1 ; с 1) с собственным значением 7. Можно доказать, что матрица оператора А в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
где l i - собственные значения этой матрицы. Верно и обратное: если матрица А в некотором базисе является диагональной, то все векторы этого базиса будут собственными векторами этой матрицы. Также можно доказать, что если линейный оператор имеет n попарно различных собственных значений, то соответствующие им собственные векторы линейно независимы, а матрица этого оператора в соответствующем базисе имеет диагональный вид. Поясним это на предыдущем примере. Возьмем произвольные ненулевые значения с и с 1 , но такие, чтобы векторы Х (1) и Х (2) были линейно независимыми, т.е. образовали бы базис. Например, пусть с = с 1 = 3, тогда Х (1) = (-2; 3), Х (2) = (2; 3). Убедимся в линейной независимости этих векторов: 12 ≠ 0. В этом новом базисе матрица А примет вид А * = . Чтобы убедиться в этом, воспользуемся формулой А * = С -1 АС. Вначале найдем С -1 . С -1 =
Квадратичной формой
f(х 1 , х 2 , х n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом: f(х 1 , х 2 , х n) = Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы . Это всегда симметрическая матрица (т.е. матрица, симметричная относительно главной диагонали, a ij = a ji). В матричной записи квадратичная форма имеет вид f(Х) = Х Т AX, где В самом деле
Например, запишем в матричном виде квадратичную форму . Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы - половинам соответствующих коэффициентов квадратичной формы. Поэтому
Пусть матрица-столбец переменных X получена невырожденным линейным преобразованием матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х T АХ = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y. Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А * = C T AC. Например, найдем квадратичную форму f(y 1 , y 2), полученную из квадратичной формы f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 линейным преобразованием .
Квадратичная форма называется канонической
(имеет канонический вид
), если все ее коэффициенты a ij = 0 при i ≠ j, т.е. Ее матрица является диагональной. Теорема (доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования. Например, приведем к каноническому виду квадратичную форму Для этого вначале выделим полный квадрат при переменной х 1: f(х 1 , х 2 , х 3) = 2(x 1 2 + 2х 1 х 2 + х 2 2) - 2х 2 2 - 3х 2 2 - х 2 х 3 = 2(x 1 + х 2) 2 - 5х 2 2 - х 2 х 3 . Теперь выделяем полный квадрат при переменной х 2: f(х 1 , х 2 , х 3) = 2(x 1 + х 2) 2 - 5(х 2 2 + 2* х 2 *(1/10)х 3 + (1/100)х 3 2) + (5/100)х 3 2 = Тогда невырожденное линейное преобразование y 1 = x 1 + х 2 , y 2 = х 2 + (1/10)х 3 и y 3 = x 3 приводит данную квадратичную форму к каноническому виду f(y 1 , y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 . Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называют законом инерции квадратичных форм. Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х 2: f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 - х 2 х 3 = -3х 2 2 - х 2 х 3 + 4х 1 х 2 + 2x 1 2 = -3(х 2 2 + Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы , равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях. Квадратичную форму f(X) называют положительно
(отрицательно
) определенной
, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е. f(X) > 0 (отрицательна, т.е. Например, квадратичная форма f 1 (X) = x 1 2 + х 2 2 - положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная форма f 2 (X) = -x 1 2 + 2x 1 х 2 - х 2 2 - отрицательно определенная, т.к. представляет ее можно представить в виде f 2 (X) = -(x 1 - х 2) 2 . В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств). Теорема . Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны). Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны. Главным (угловым) минором k-го порядка матрицы А n-го порядка называют определитель матрицы, составленный из первых k строк и столбцов матрицы А (). Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным. Например, исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 + 3х 2 2 . Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = 2 > 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма - положительно определенная. Исследуем на знакоопределенность другую квадратичную форму, f(х 1 , х 2) = -2x 1 2 + 4х 1 х 2 - 3х 2 2 . Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 . Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид Одно из этих чисел отрицательно, а другое - положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака). Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = 2 > 0. Главный минор второго порядка D 2 = = -6 - 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен). Определение 9.3. Вектор х называется собственным вектором матрицы А , если найдется такое число λ, что выполняется равенство: Ах = λх , то есть результатом применения к х линейного преобразования, задаваемого матрицей А , является умножение этого вектора на число λ . Само число λ называетсясобственным числом матрицы А . Подставив в формулы (9.3) x` j = λx j , получим систему уравнений для определения координат собственного вектора:
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:
получим уравнение для определения собственных чисел λ , называемое характеристическим уравнением . Кратко его можно представить так: | A - λE | = 0, (9.6) поскольку в его левой части стоит определитель матрицы А-λЕ . Многочлен относительно λ | A - λE | называется характеристическим многочленом матрицы А. Свойства характеристического многочлена: 1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство. 2) Если матрица А линейного преобразования является симметрической (т.е. а ij =a ji ), то все корни характеристического уравнения (9.6) – действительные числа. Свойства собственных чисел и собственных векторов: 1) Если выбрать базис из собственных векторов х 1 , х 2 , х 3 , соответствующих собственным значениям λ 1 , λ 2 , λ 3 матрицы А , то в этом базисе линейное преобразование А имеет матрицу диагонального вида:
2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы. 3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид. Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (9.5) следует, что если х (1) ={x 1 ,x 2 ,x 3 } – собственный вектор, соответствующий λ 1 =-2, то
Подставив в систему (9.5) λ 2 =3, получим систему для определения координат второго собственного вектора - x (2) ={y 1 ,y 2 ,y 3 }:
Для λ 3 = 6 найдем собственный вектор x (3) ={z 1 , z 2 , z 3 }:
х (3)
= Лекция 10. Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду. Определение 10.1. Квадратичной формой действительных переменных х 1 , х 2 ,…,х n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени. Примеры квадратичных форм: (n = 2), (n = 3). (10.1) Напомним данное в прошлой лекции определение симметрической матрицы: Определение 10.2. Квадратная матрица называется симметрической , если , то есть если равны элементы матрицы, симметричные относительно главной диагонали. Свойства собственных чисел и собственных векторов симметрической матрицы: 1) Все собственные числа симметрической матрицы действительные. Доказательство (для n = 2). Пусть матрица А
имеет вид: (10.2) Найдем дискриминант: Следовательно, уравнение имеет только действительные корни. 2) Собственные векторы симметрической матрицы ортогональны. Доказательство (для n = 2). Координаты собственных векторов и должны удовлетворять уравнениям. |
| Читайте: |
|---|
Новое
- «31 спорный вопрос» русской истории: житие императора Николая II
- Лечебные свойства корня лопуха и его широкое применение в домашних условиях
- Природные ресурсы западной сибири
- Совместимость петуха и змеи в любовных отношениях и браке Он петух она змея совместимость
- Чемерица черная: прекрасная и опасная Противопоказания и побочные действия
- Чем интересна Свято-Михайло-Афонская Закубанская пустынь?
- Порционная сельдь под шубой на праздничный стол
- К чему снится шить во сне
- Примета — разбить зеркало случайно: что делать, если оно треснуло
- Самостоятельные заговоры на удачу и деньги

 , X
– некоторая матрица–столбец,
высота которой совпадает с порядком матрицы A
. .
, X
– некоторая матрица–столбец,
высота которой совпадает с порядком матрицы A
. . .
.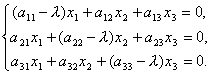






 = 0
= 0 ,
,



 . (9.5)
. (9.5)
 (9.7) Доказательство этого свойства следует из определения собственных векторов.
(9.7) Доказательство этого свойства следует из определения собственных векторов. (1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
³ - 7λ
² + 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6. - совместная, но неопределенная система. Ее решение можно записать в виде х
(1)
={a
,0,-a
}, где а – любое число. В частности, если потребовать, чтобы |x
(1)
|=1, х
(1)
=
- совместная, но неопределенная система. Ее решение можно записать в виде х
(1)
={a
,0,-a
}, где а – любое число. В частности, если потребовать, чтобы |x
(1)
|=1, х
(1)
=  , откуда х
(2)
={b,-b,b
} или, при условии |x
(2)
|=1, x
(2)
=
, откуда х
(2)
={b,-b,b
} или, при условии |x
(2)
|=1, x
(2)
=  , x
(3)
={c
,2c,c
} или в нормированном варианте
, x
(3)
={c
,2c,c
} или в нормированном варианте . Составим характеристическое уравнение:
. Составим характеристическое уравнение:




